Definitionsmenge
Inhaltsverzeichnis
\(\\\)
Definitionsmenge und Wertemenge
Wichtige Mengen in der Analysis sind die Definitionsmenge (Definitionsbereich) und die Wertemenge (Wertebereich). Dabei bezeichnet, wie hier mit einer Funktion \(f\) dargestellt, die von 1 bis 7 definiert ist,

der Definitionsbereich die Menge aller für die Funktion zulässigen \(x\)-Werte.
\( \quad \mathbb{D} \; = \; \bigl\{ x \, \big| \, 1 \leq x \leq 7 \; , \; x \in \mathbb{R} \bigr\} \)
\(\\\)
Entsprechend ist der Wertebereich die Menge aller für die Funktion zulässigen \(y\)-Werte.
\( \quad \mathbb{W} \; = \; \bigl\{ y \, \big| \, 0{,}5 \leq y \leq 6{,}5 \; , \; y \in \mathbb{R} \bigr\} \)
\(\\\)
Im obigen Beispiel handelt es sich um eine Funktion mit eingeschränkten Definitionsbereich. Meist haben wir es aber bei ganzrationalen Funktionen, also mit Funktionen von der Form
\( \quad f(x) \; = \; a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + \dots + a_2x^2 + a_1x + a_0 \)
\(\\\)
zu tun mit Funktionen, die über den ganzen Bereich der reellen Zahlen definiert sind. Zum Beispiel
\( \quad f(x) \; = \; 2x^3 + 7x^2 - 4x + 9 \; \text{ mit } \; \mathbb{D} = \mathbb{R} \)
\(\\\)
Es gibt jedoch Funktionen, die von Natur aus nicht über den ganzen Bereich der reellen Zahlen definiert sind. Dabei sind vor allem zu nennen die
- gebrochen-rationalen Funktionen
- Wurzelfunktionen
- Logarithmusfunktionen
\(\\[2em]\)
Nenner ist Null
Das Teilen durch Null ist nicht definiert.Das heißt, dass in einem Bruch der Nenner nicht den Wert Null annehmen darf.
Betrachten wir die folgende gebrochen-rationale Funktionsgleichung :
\( \quad f(x) \; = \; \frac{x - 1}{x^2-x-6} \)
\(\\\)
Wie bestimmen wir hier den Definitionsbereich? Dazu setzen wir den Nenner gleich Null.
\( \quad \begin{array}{ r c l } 0 & = & x^2 - x- 6 \\[16pt] x_{1,2} & = & - \frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q} \\[8pt] x_{1,2} & = & - \frac{-1}{2}\pm \sqrt{\left( -\frac{1}{2}\right)^2-(-6)} \\[8pt] x_{1,2} & = & \frac{1}{2}\pm \frac{5}{2} \\[16pt] x_{1} & = & 3 \\[6pt] x_{1} & = & -2 \\ \end{array} \)
\(\\\)
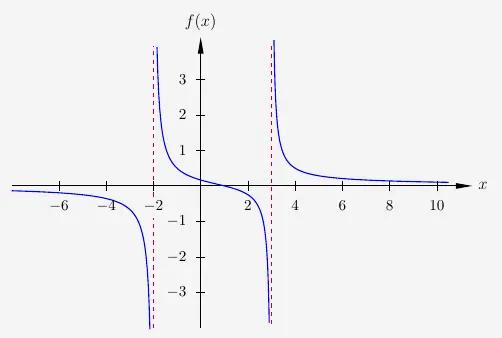
Wir sehen also, dass die gebrochen-rationale Funktion bei \(x=-2\) und \(x=3\) nicht vorkommt und erhalten den Definitionsbereich
\( \quad \mathbb{D} \; = \; \mathbb{R} \setminus \{-2, 3 \} \)
\(\\[2em]\)
Wurzelfunktionen
Bei der Wurzelfunktion
\( \quad f(x) = \sqrt{x-2} \)
\(\\\)
darf die Diskriminante, also der Wurzelinhalt, nicht negativ sein. Wir berechnen das, was gelten darf mit
\( \quad \begin{array}{ r c l l } x - 2 & \geq & 0 & | +2 \\[6pt] x & \geq & 2 \end{array} \)
\(\\\)
und erhalten den Definitionsbereich
\( \quad \mathbb{D} = \{ x | x \geq 2 \; , \; x \in \mathbb{R} \} \)
\(\\[2em]\)
Logarithmusfunktionen
\( \quad f(x) = ln(x) \, \rightarrow \text{ logarithmus naturalis } \)
\(\\\)
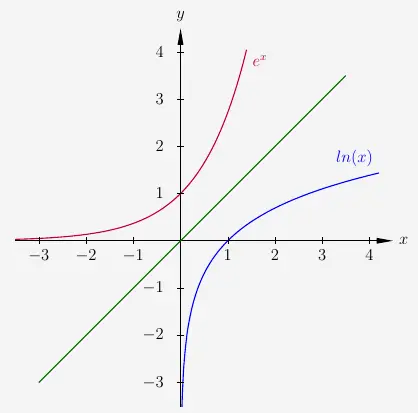
ist die Umkehrfunktion von der \(e\)-Funktion.
Das heisst: Ebenso wie die \(e\)-Funktion nie die \(x\)-Achse erreicht, erreicht die Logarithmusfunktion
\( \quad f(x) = ln(x) \)
nie die \(y\)-Achse und es gilt dann für den Definitionsbereich:
\(\quad \mathbb{D} = \bigl\{ x \bigl{|} x > 0 \} \)
\(\\[1em]\)